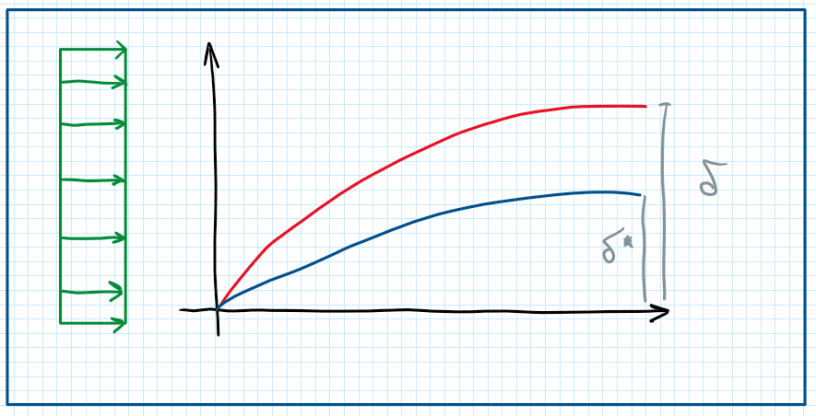
Considering a uniform flow aligned in direction X. At a specific moment a flat blade is introduced in the flow domain. The flow is a laminar one which its boundary layer thickness is given by:
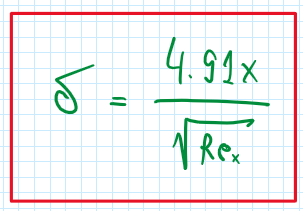
Introduction of a flat plate in a flow with a given velocity field implies that, the mean velocity in the vicinity of the solid wall is decreased. Mass conservation requires that streamlines above the boundary layer thickness are bended upward. The displacement of the streamlines is called displacement thickness. This is thinner than the boundary layerand this is usually given by:

As can be seen horizontal laminar flow exhibits this streamlines configuration. In other words, horizontal steam streamlines without perturbationl.This changes when a flat and very thin plate is introduced in this flow.

There are two immediate effects due to the inclusion of a flat plate. First, the flow is disturbed, the streamlines are not anymore horizontal.The second effect is observed by the lines of the velocity profiles.
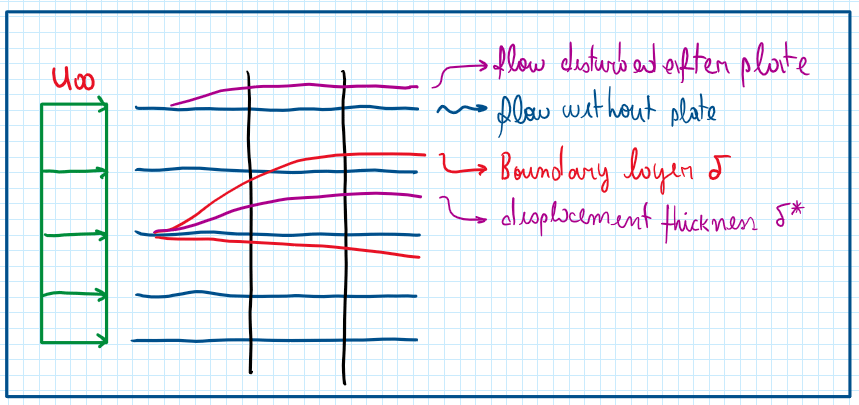
As can be seen, there is a region where the mass flow is lost,which is highlighted.As the mass must be conserved,a reaction on the streamlines is observed which is a small deviation relative to the horizontal flow streamline.Hence the presence of a flat plate in a flow represents an obstruction of the flow.Displacement thickness therefore is the distance between the horizontal streamline and the bended streamline.

Considering a flow with a given velocity (Uinfinity), the displacement thickness allows that mass flow lost due to the obstruction equals to the mass flow of the deviated one, thus:
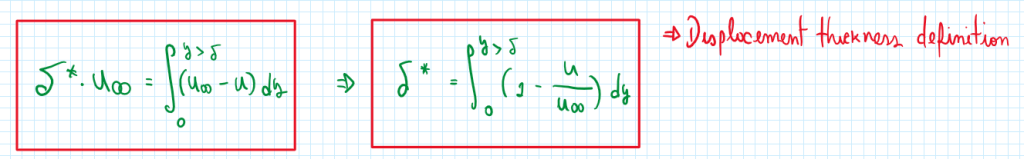
Hence a boundary layer over a flat plate is exposed to the streamlines which are deviated due to the presence of the flat plate. The boundary layer is given as a function of the flow velocity. The assumptions of the effects of the flat plate always consider the constant density.
Direction integration method
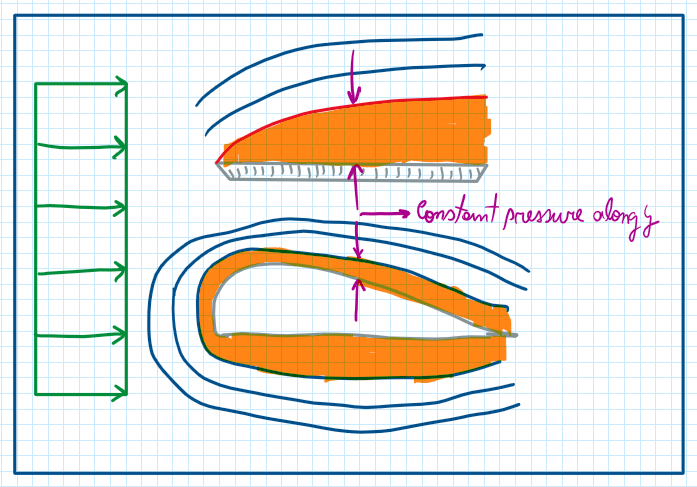
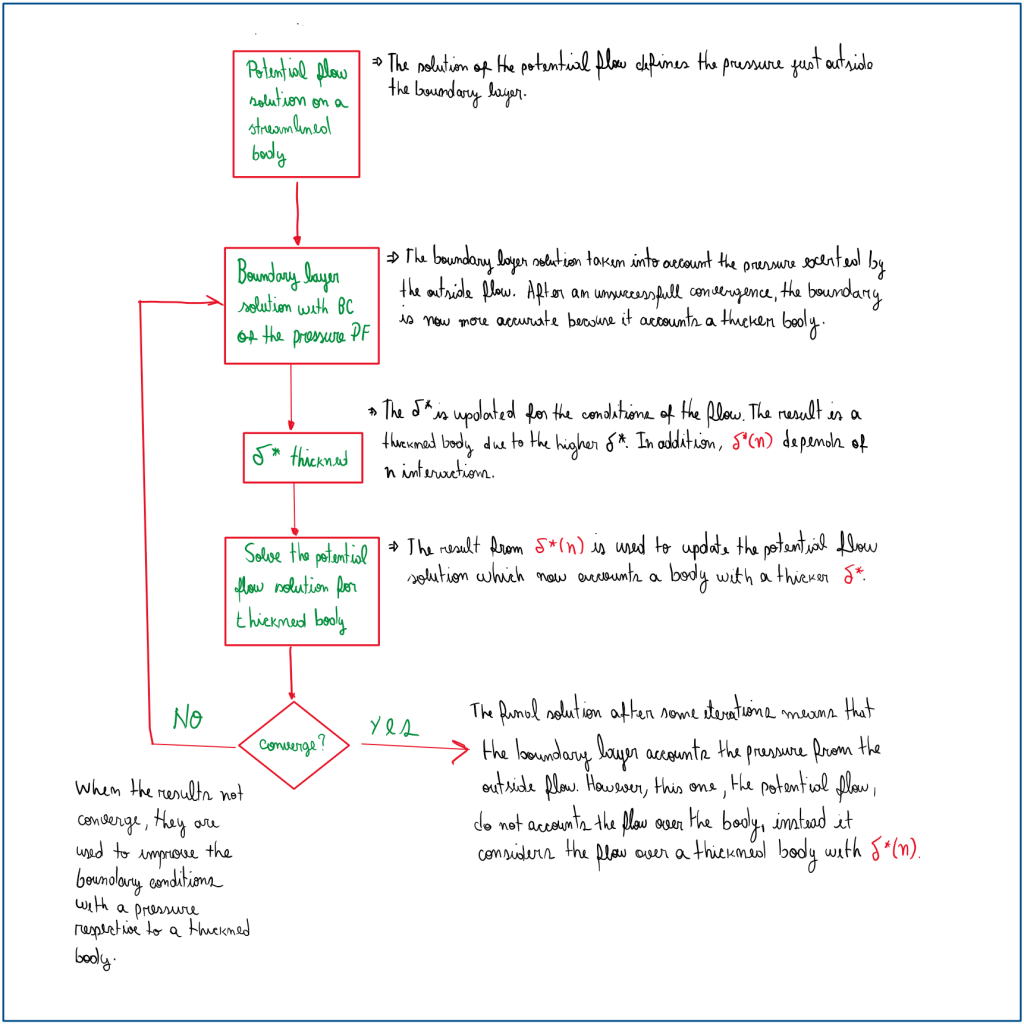
The main idea behind the direction integration method begins with the application of the Navier Stokes equation. This can be used in cases where the density is in function of the temperature and pressure coma density is in function of pressure and density is constant. For a boundary lawyer with constant density the diversions of the velocity field is zero and the curl of the velocity field is also zero , this last one can be solved by potential flow solutions coma because it is irrotational. The boundary lawyer problems can be solved by boundary lawyer theory. Outside the boundary layer there is a flow with irrotational characteristics. The potential flow solution can be applied to solve this problem. In addition the pressure can also be evaluated by potential flow. Hence, outside the boundary layer there is vorticity, but at the very far distance from the surface there is no vorticity. So the pressure is provided by the outer flow. As the name suggests the method uses interaction to obtain a convergence of the information shared between the potential flow and boundary layer solution. This is necessary, because the pressure exerted by the potential flow must be used as boundary layer conditions for the main lawyer. In addition, boundary layer changes when the displacement thickness gets thicker.
References
- Stalio, Enrico. Aerodynamics. October, 2021;
- http://www.aerodinamica.unimore.it