On the previous articles it were developed all the calculations about the longitudinal dynamics of rear and four wheel drive vehicles. Some details are common between those two kinds of drivetrains. For instance the effects of the inertia. In fact whether this is analyzed more deeply it is found the concepts of equivalent mass and inertia. This article will approach the main details about these two parameters and their influnces on the driveline.

Equivalent mass

The concept of the equivalent mass is a reduction of all loads and masses of the vehicle in just one parameter. For this firstly it is required consider the equation for the torque quested at the wheels.

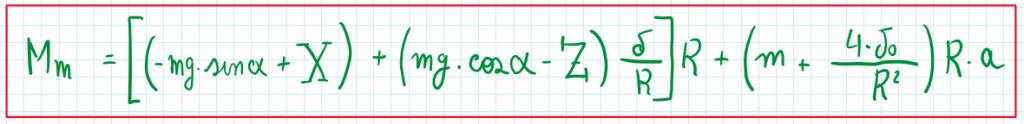
Observing that the required torque equation Mm already considers the reduced inertia of the entire axles. The same approach is required the from the engine. This one has its on torque curve and internal inertia, both must be accounted. Thus:

So, the requested torque must be equal to the torque provided by the engine reduced by internal loads and accounting also the differential ratio Tau P and the gearbox ratio on a respective gear Tau C. Then the requested torque at the wheels equation (Mm) can be found. This is a function of the engine torque, its inertia, the gearbox ratio, the differential ration and the efficiency of the driveline (neta t). Through this equation it is possible to understand how different gears inflicts on the equivalent mass. Hence, considering a simplification of the driveline which the entire gearbox and differential are reduced to just one inertial device the following arrange can be presented.

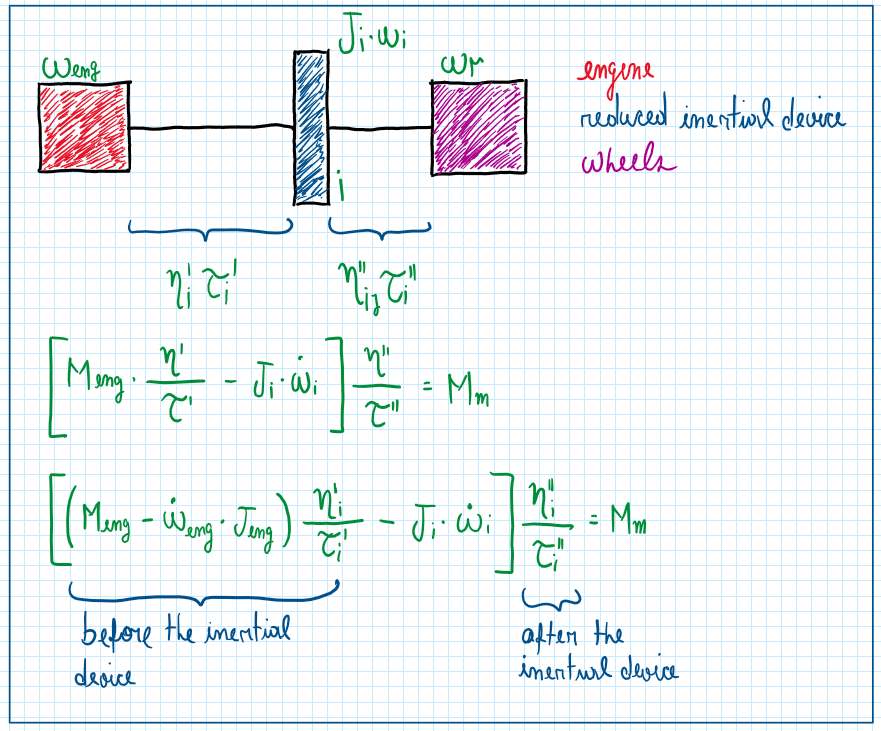
The objective of this arrange is to illustrate and simplify the entire drivetrain. The equation of the inertial component is represented by J*Omega-dot and this account the reduced inertia of the all components after the engine and before the wheels. The required torque equation must be updated. Hence there is the inertia before the device, which multiplied by the ratio neta’ by Tao’ and the relation of the wheels. In the end all these are multiplied by the components after the device, which is represented by the ratio between neta” and Tau”. After these calculations it is possible to write the following relations:

These relations can be written , because the scheme assume that there is a rigid connection between those components. Hence , the next update for the required torque at the wheel equation is:

Even the powertrain comprises several components, for instance, shafts and hubs, these must be accounted on the requested torque equation. For this a sum is used to emulate these components on the driveline, thus the equation of the torque requested at the wheel become:

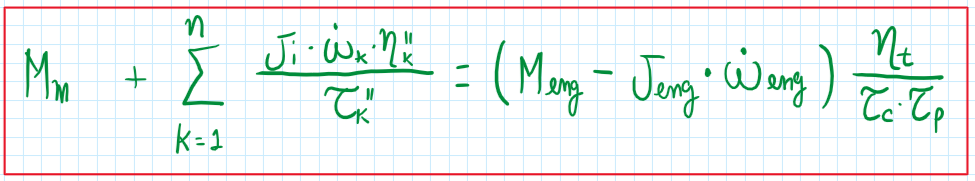
Understanding that the vehicle inertia is accounted by the mass times the acceleration (m times a), it is possible to follow some assumptions:

At this point of the calculation a new assumption is valid and introduced. The wheel speed can expressed in other form.

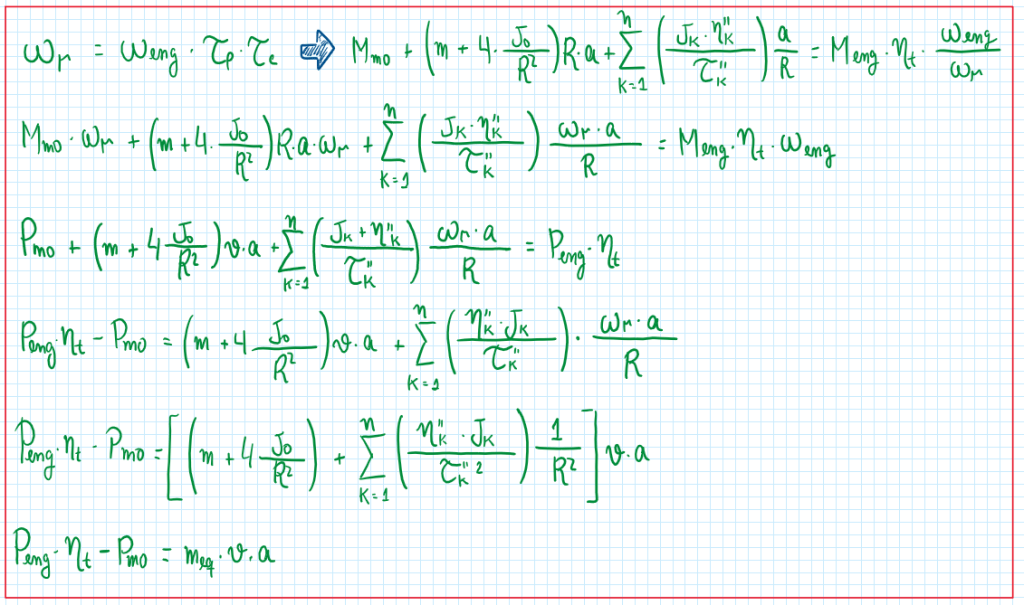
Finally after this calculation it is possible to obtain an important equation. Its first component is the excess power, which is given by the left side portion of the equation. It accounts the total efficiency of the driveline deduced by the power required for the constant speed travel (P_mo). This is equal to the equivalent mass (m_eq) times the velocity and the acceleration. Moreover it is important to analyze the equivalent mass equation.

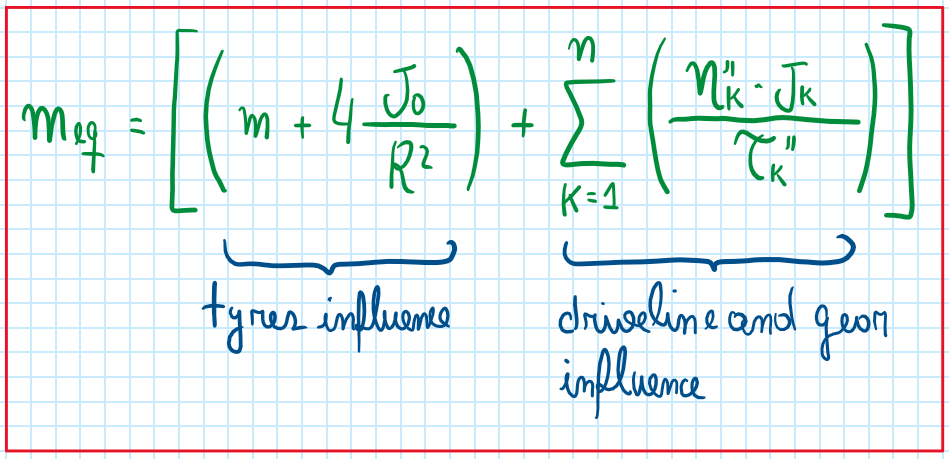
As can be seen the reduced mass or equivalent mass accounts two important terms. First , the portion of the equation which accounts the tires effects and the portion that is respective to the driveline and the gear in use. This last one is the most important, because it is constantly changing the equivalent mass of the vehicle. Each gear has its own ratio Tao, efficiency eta and polar moment of inertia J. in addition the equivalent mass can be further simplified focusing on components before and after the secondary shaft of the gearbox.

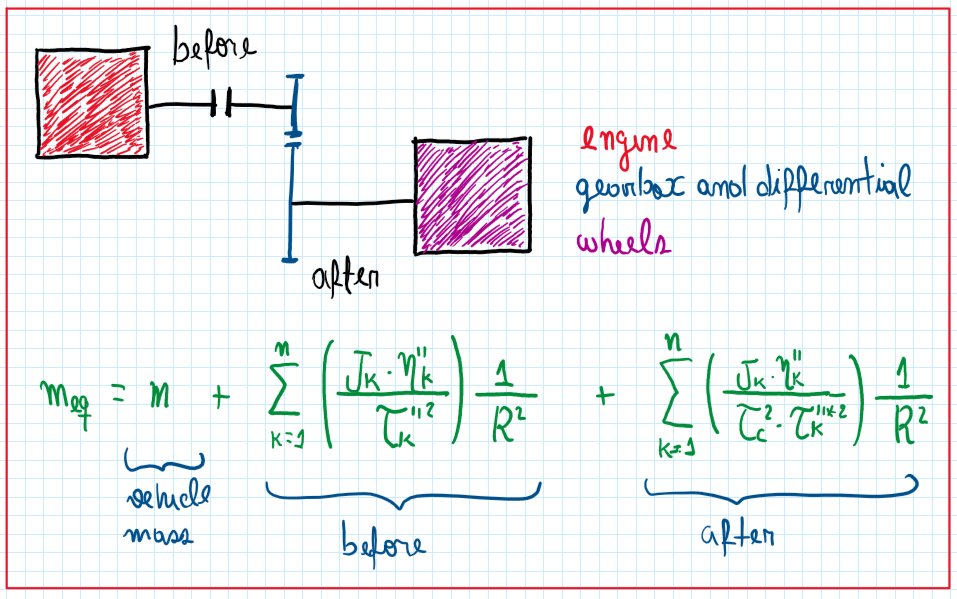
Now the equivalent mass equation is split in two parts relative to the components before and after the gearbox. The equation is composed by three portions . The first one is equivalent to the mass of the vehicle, the second is equivalent to components before the gearbox and the last one the contributions of the wheels and the components after the gearbox. It can be noted that in this portion there is a term TaoK”*, which is different from the same term on the portion of components before the gearbox and usually is substituted by Tao P. Therefore the effect of certain gear on the equivalent mass is even more easy to be read with the following manipulation:

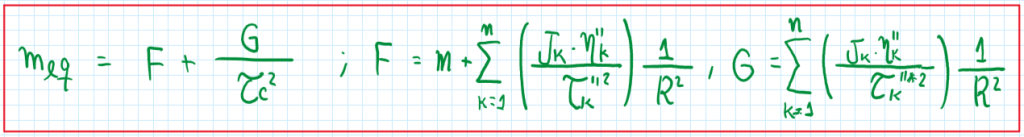
Finally it is clear that each moment which are lower gear (1st, 2nd and 3rd) is shifted, the equivalent mass increases dramatically.

References

• Guiggiani, Massimo. The Science of Vehicle Dynamics. Handling, Braking, and Ride of Road and Race Cars. New York, Springer, 2014;
• GILLESPIE, Thomas D, Fundamentals of Vehicle Dynamics, Warrendale, Society of Automotive Engineers, 1992. 470p.