There are many kinds of tires, even if it is only considered the automotive applications, still there are many tire variations. Hence, some standards were developed to classify tires and guide customers to buy and use the correct tire for their applications. This article propose a brief review about the tire classification and references.

Basic standards

For road tires, ECE and DOT standards were introduced to classify the tire type. These define that tires must have a code, usually called reference, with informations as tire manufacturer, size, application, structure, load rating and speed category. Figure 1 illustrates a common example of a road vehicle tire:

For race tires the reference is similar, but there are some differences due to the purpose of a race tire. Basically, a race tire must provide the highest friction coefficient as possible. In other words, the highest grip. For this the tread should as flat as possible, thus the sidewalls should be stiff. Race tires reference sometimes refers the width as the tread width, instead the nominal tread.

Figure 2 illustrates a tire used in the Indy 500 event. It is possible to visualize the reference in millimeters and in inches. Figure 3 illustrates that different references seen in Figure 2 describes different informations.

As can be seen, the standard in millimeters describes this tire by the nominal tread while the standard in inches describes only the tread itself, in other words, the part of the tire that really is in contact to the asphalt.

Hence, for racing purposes, the number that describes width, in some racing series, describes the tire contact patch width. This is the most important portion of a tire, specially for race cars. The number after the slash describes the tire nominal diameter.

Tire reference

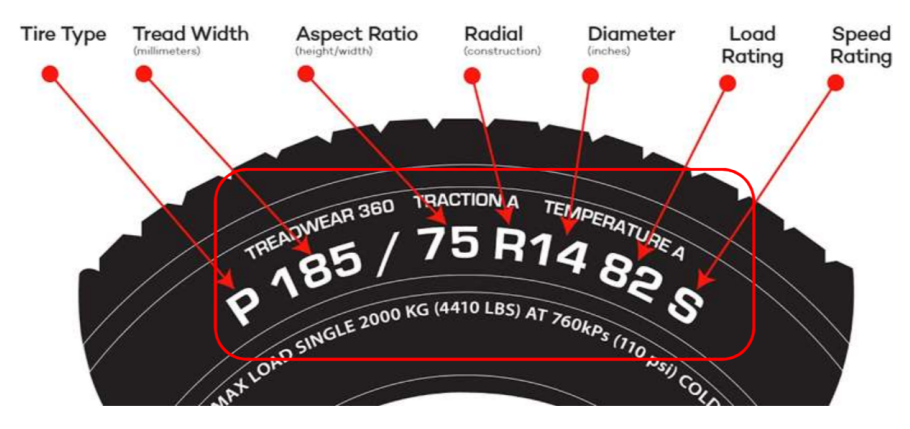
The main tire parameters are listed below:

• Nominal width;
• Aspect ratio (AS);
• Tire construction: Cross or radial ply;
• Tire rim diameter;
• Load index;
• Speed index;
• Tire type.

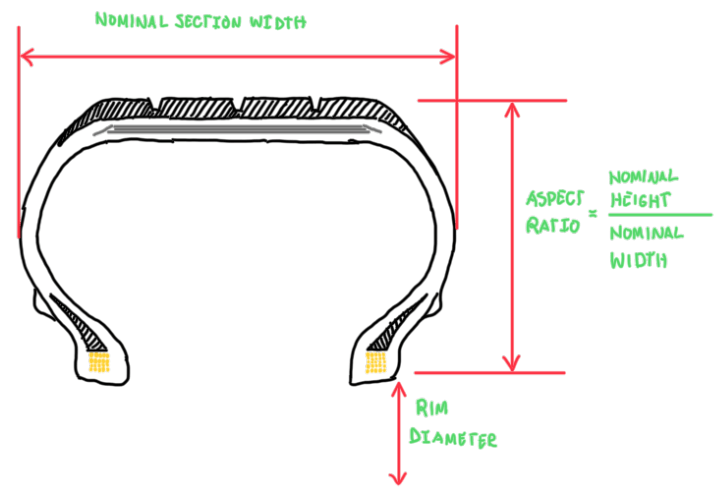
Tire width and aspect ratio

The nominal width is basically the value of the tire width at nominal pressure, which the length between inner to the outer board of the tire. Actually, tire pressure has effects on the tread width. It is supported by the sidewalls that ensure its flatness. The height of the sidewalls can be calculated by the aspect ratio, which is the percentage of the sidewall relative to the nominal width. The importance of the aspect ratio (AS) is the tire capacity to absorb shocks and vibrations on the tread. As high AS, higher the shock absorption, but at the cost of the tread flatness, because high sidewalls are flexible. In the opposite case, a low aspect ratio provides a stiffer tread, but at a cost of shock absorption. However, it is possible to visualize that in racing applications that there are some tires with AS reasonably high, but these still are possible to generate and support high lateral forces and wheel loads. The reason is the material which those tires are made, that provides a very stiff sidewall and flat tread.

Tire construction

Usually, previous the rim diameter there is the word R, this refers to the tire construction. Tires are made by internal steel wire belt, its layers are called plies. The first pneumatic tires had a belt called cross-ply. Hence, the belt was composed by layers that cross themselves and this gave to those tires a circular shape of the contact patch, similar to a motorbike tires. For that period, this was useful, because roads were not properly flat. However, as roads evolve and became more flat and smoother, those kinds of tires became obsolete. This occurs because the cross-ply construction provides a very flexible and round shape tread, which distorts too much. The modern tire has radial plies, thus the layers of the belt are disposed at the same orientation of the tire rotation axis. This configuration provides a flatter tread, as a result this tire generates more grip, because the tread has a more uniform contact with the surface. In addition, the sidewalls and the tread are stiffer, which makes this tire able to hold the tread at the correct position. The only problem with this construction is the sensitivity to camber. Hence, modern cars must have a rigid maintenance respective to wheel alignment.

Rim diameter

The rim diameter is described after the tire construction code, or only at a brief space from the tire dimensions. This parameter is used to calculate the tire diameter, which is the overall one. Actually, the rim diameter has effect in many factors of the car design, but concerning to the wheel assembling, the rim size is defined according to brake disc and the upright sizes. Another important aspect of rim diameter is the vehicle dynamics. As bigger the rim, smaller will be the tire in terms rubber amount. The inner volume for big rim tires are small, thus for the same amount of air inside the tire chamber, the pressure is considerably higher. Therefore, tires with big rims (Φ>17″) usually are stiff and provide fast steering responses, but at cost of a lower capability of shocks and vibration absorption.

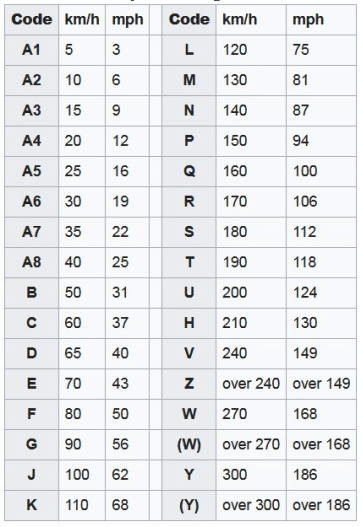
Tire speed index

The speed index is directly related to the tire construction and the temperature which this can hold during operation. Actually, as fast the car is traveling, the tread suffer waves that propagates over the tire circumference. The tire construction must be stiff enough to hold the contact patch at the surface, which is the main function of the tire carcass. The problem is the so called static standing waves (Figure 6), because tires are deformable as the air inside of them. The evaluation of these waves is made by the Turner number, which is written below:

C_W = √(t_c/ρ_c) [m/s] ; tc [(N∙L^-2)/L] = [(M∙L∙s^-2)/(L²/L)] ; ρ_c [(M∙L^-2)/L]

λ = k√[1 – (V/C_W)²] = k√{1 – [ρ_c∙(Ω∙R_u)²]/t_c}

N_t = V/C_W = Ω∙R_u/[√(t_c/ρ_c)]

Where tc is the crown circumferential tension per unit width, ρc is the crown density per unit width, λ is the wave length and V is the tread peripheral speed and N_t is the Turner number. This parameter is a kind of Mach number for tires, because it defines how much a tire is prone to generate waves. As can be seen, N_t depends on V and C_W. This last parameter is a ratio between t_c and ρ_c. In other words, the wave propagation around the circumference is directly dependent to V, but can be reduced by the tire structure and material parameters, which are accounted by C_W.

Example – Speed Index

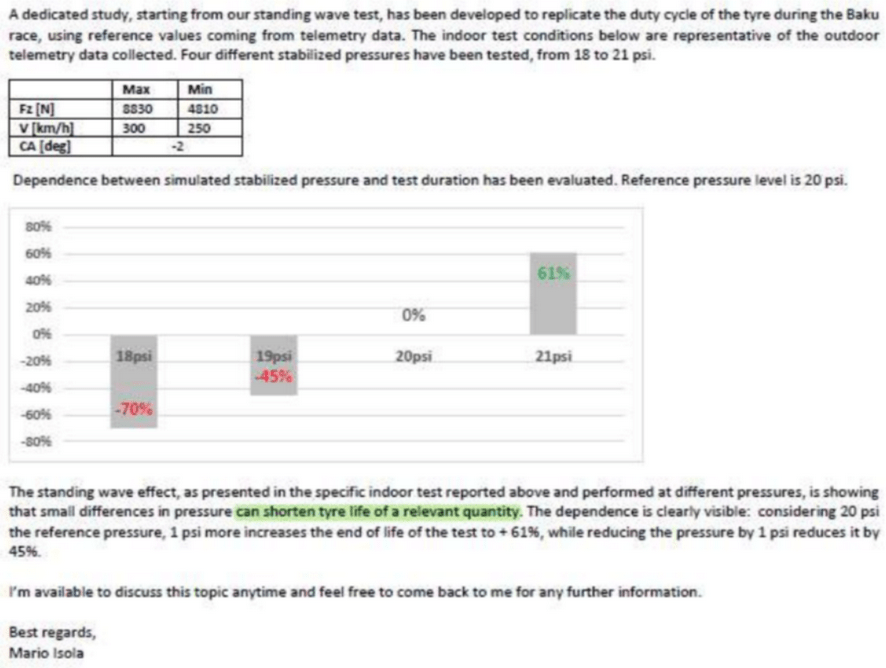
The example illustrated at Figures 7 and 8 is the report about the tire blow that occurred in the Max Verstapen Red Bull car during 2021 Azerbaijan Formula One Grand Prix. The Red Bull driver did not finished the race due to a tire problem. After the Red Bull team complaining about the tire quality, Pirelli presented a report that clearly mentioned the static standing waves (Figures 7 and 8) and their increase with the speed. In addition, Pirelli claimed that the cut at the tire shoulder weakened the tire shoulder. It is important to mention that this is a critical point of the tire, because it is the interface between tread and sidewalls. However, this is not related with standing waves, instead it is related to the inflation pressure. To support their argument, Pirelli tested four tires with different inflation pressure to illustrate and prove how tires wit excessively low pressure (P < 20 psi) expose it to problems as the one from Red Bull. F1 teams sometimes with lower pressures to obtain more grip from the tires. However, tire suppliers usually inform the teams the tire characteristics, which one of them is the minimum inflation pressure.

Speed index table

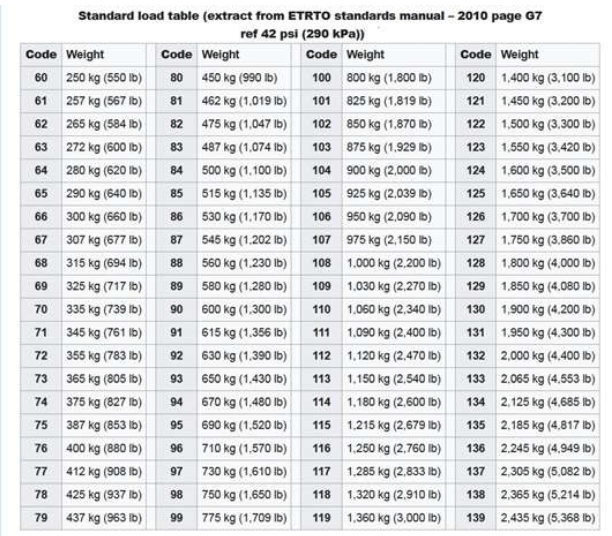
Tire load index

Another important information is the load index which is a number that is written at the tire sidewall together with a letter, which is the speed index. Tires loads are defined by the amount of air inside the tire. Hence, tire with a low aspect ratio may not provide a high load capacity even though the inflation pressure is high. Once the tire information is known, it is also possible to calculate the tire load capacity:

L = K∙0.425∙P^0.585∙S^1.39∙(D+S)

Where K is a service factor usually given by 1 when it oscillates from 0.9 to 1.1, P is the inflation pressure, S is the tire section width and D is the nominal rim diameter. All of these parameters defines the load capacity at a given pressure. Hence, in the absent of the load index table, by the information on the sidewall, it is possible to calculate at a given pressure.

Load index table

Examples

14 inch × 25.4 mm/inch = 355.60 mm → Rim diameter

185 mm × 0.75 = 138.75 mm → Sidewall height

355.60 mm + (2×138.75) = 494.35 mm → Total wheel diameter

2πr = 2π∙(494.35/2) = 1553.0463 mm → Tape ratio

185∙1553.0463 = 287313.51 mm² → Tape area

82S → 475 kg and 180 km/h

Figure 5 illustrate a common tire for road cars, while Figure 11 also illustrates a similar example, but with a variation the previous nomenclature.

15 inch × 25.4 mm/inch = 381.0 mm → Rim diameter

0.70∙205 mm = 143.50 mm → Sidewall height

381 + (2∙143.50) = 668.00 mm → Tire diameter

2πr = 2π∙(668/2) = 2098.584 mm → Tape ratio

2098.584 × 205 = 430209.698 mm² → Tape area

90w → 600 kg and > 270 km/h → Speed and load index

References

• Haney, Paul. The Racing & High-Performance Tire – Using the Tires to Tune for Grip & Balance. TV Motorsports, SAE, January, 2003;
• Dias, A. L. Funcionamento e detalhes dos pneus automobilísticos. Published at January 21st 2019 at Carros Infoco Website.