A Φ = 10 cm diameter cylinder is immersed in an air flow of a free stream velocity U_∞ = 6 m/s at the horizontal direction i.

First part

The first part of the exercises assumes the potential flow hypothesis, thus it is important to remember that this flow irrotational, ω = 0 (Cover Figure).

Question 1 – Calculate CP at the wall (r = 5 cm) and θ = 3π/4

Re = (U_∞∙x)/ν

q_∞ = ½∙ρ∙U_∞ = ½∙1.2∙6² = 21.6 Pa

C_P = 1 – 4∙sin²(θ) = 1 – 4∙sin²(3π/4) = 1 – 4∙(√2/2)² = 1 – 2 = – 1

Question 2 – Calculate the velocity vector at the same point, but expressed in cartesian and cylindrical components

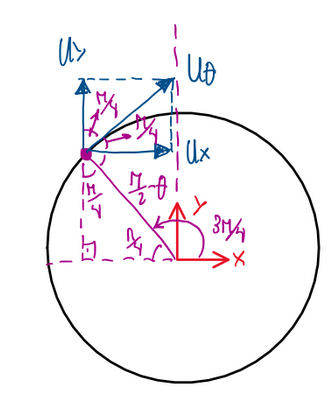
v = (U_x , U_y) → Cartesian coordinates

v = (U_r , U_θ) → Cylindrical coordinates

U_θ = – 2∙U_∞∙sin(θ) = -2∙6∙sin(3π/4) = – 6√2 m/s

U_y = U_θ∙sin(π/4) = – 6√2∙(√2/2) = – 6 m/s

U_x = U_θ∙cos(π/4) = – 6√2∙(√2/2) = – 6 m/s

v = (- 6 , – 6) m/s

v = (0 , – 6√2) m/s

Question 3 – Calculate the vorticity at (r = 5 cm , θ = 3π/4)

Since it was assumed the hypothesis of potential flow, the flow is irrotational, thus the vorticity is ω = 0.

Comments

The pressure coefficient for the potential flow around a cylinder is obtained from the Bernoulli equation, which is C_P = 1 – 4sin(θ). Since potential flows describe that the velocity is given in cylindrical coordinates, v = (Ur = 0 , U_θ = – 2∙U∙sin(θ)). In addition, the velocity components in cartesian coordinates are function of the component U_θ. The vorticity of this air flow is ω = (0 , 0), because potential flows are irrotational.

Second part

The second part of this exercise proposes that the cylinder is placed in an automotive wind tunnel. The distance from the belt is h = 0.20∙Φ. The lift and the drag coefficients were measured, CL = 0.40 and CD = 1.0, respectively. The separation occurs at the upper and the inner surfaces of the cylinder, but at different angles, θ_t = 120° and θ_b = 265°, respectively.

Question 4 – Calculate the aerodynamics force vector per unit length

L = q_∞∙C_L∙Φ = 21.6∙0.40∙0.10 = 0.864 N/m

D = q_∞∙C_D∙Φ = 21.6∙1.0∙0.1 = 2.16 N/m

F = (2.16 , 0.864) N/m

F² = 2.16² + 0.864² → F = 2.326 N/m

Question 5 – Calculate the drag component at the base (C_P,b = – 0.75)

D_b = – q_∞∫C_P,B∙(n∙i)∙dS = – q_∞∫_θb^θ_t C_P,B∙cos(θ)∙rdθ = – q_∞C_P,B∙r (sin(θ_t) – sin(θ_b))

D_b = -21.6∙(-0.75)∙(0.1/2)∙(√3/2 – 1) = 1.508 N/m

Question 6 – Calculate the lift component at the base (C_P,b = – 0.75)

L_b = – q_∞∫C_P,B∙(n∙j)∙dS = – q_∞∫_θb^θ_t C_P,B∙sin(θ)∙r∙dθ = – q_∞C_P,B∙r [-cos(θ_t) – (-cos(θ_b)]

L_b = -21.6∙(-0.75)∙(0.1/2)∙(1/2 – 0.087) = 0.334 N/m

Question 7 – Calculate the vorticity frequency since the Strouhal number St = 0.2

St = (ƒ∙D)/U_∞ → ƒ = (St∙U_∞)/D = 0.2∙6/0.1 = 12 s^-1 = 12 Hz

Conclusion

As can be seen, since the angles which the flow separates are known, it is possible to perform the integral over the cylinder surface, which is given by Δθ between the two angles. The aerodynamic force asked is the resultant from the total lift and drag, thus since drag and lift coefficients were given, it is possible to calculate it. It is interesting to notice that the drag due to the base region of the cylinder has the major percentage of the total drag.

D_%b = 1.508/2.16 = 0.698 ≃ 70%

In the case of the lift component, this value is lower.

L_%b = 0.476/0.864 = 0.551 ≃ 55.1%

Hence, the base region of the cylinder is the most important for the aerodynamics. Aero devices with a rounded shape should be analyzed with some careful. Another important conclusion is about the last question. The Strouhal number is 0.2 and the Reynolds number is 4000, which characterize the flow as laminar and subcritical.

Downloads

Download the notes of this exercise.