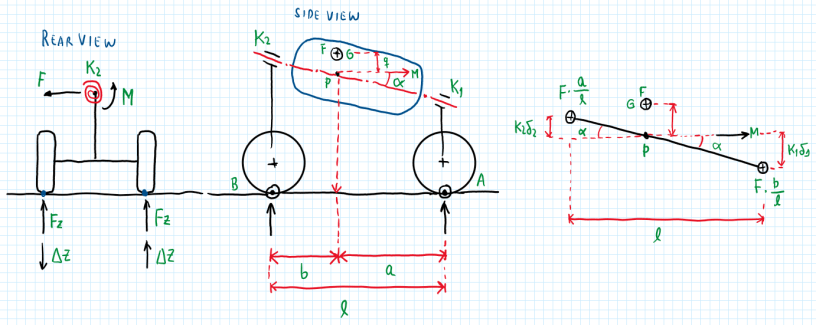
Any important dynamic evaluation in automobiles is the lateral dynamics, this field analyze the vehicle behavior during cornering. Basically there are two approaches to evaluate lateral dynamics, the roll axis approach and the without roll axis approach. Both methods adopts the same assumptions:

• Steady state cornering;
• Centrifugal force F apply it at the center of gravity during cornering.

This article aims to develops these methods and discuss about the main parameters which has direct influence on the vehicle performance during cornering.

The roll axis approach

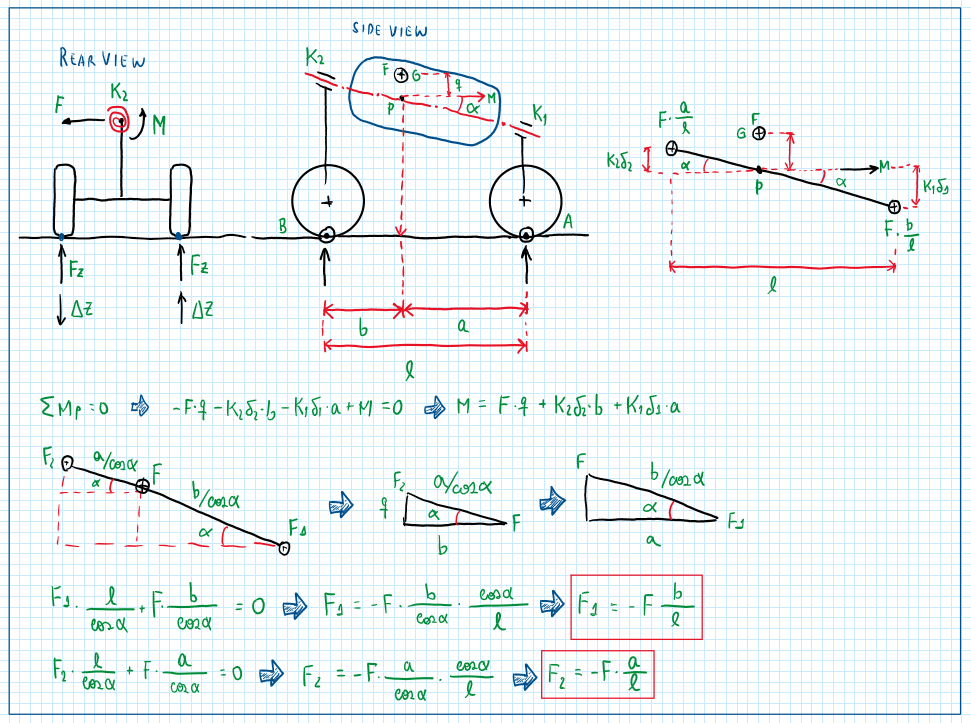
After all these calculations, the contributions of the moments can now be evaluated considering that the roll produced by an angle theta. Therefore the moment at point B is partitioned in normal and axial moments. The moment resultant is the one applied by the body on the rear axle.

The lateral load transfer given by the roll axis formula is a function of the chassis geometry, the lateral force in the total stiffness of the chassis itself and the elastic components from the suspension. This method is only applicable under the assumption of the constant track.

The no-roll axis approach

In this approach the main point is there analysis of 3 movements of the center of mass G, they are bounce, roll and pitch. Those movements and the suspension displacements are represented by column vectors. For computing the lateral load transfer it is required to link those vectors in a way that they are at the same coordinate reference. Therefore the following connection can be done:

The static vertical translation do not account lateral one. However during a vertical travel each suspension also is exposed to lateral forces. Thus, the sum of the forces are given by:

Suspensions and wheels equations

The first sum of forces are respective to the suspension 1 and wheel 1. The equation above is about the vertical displacement of this wheel. All the terms arise when the car is cornering. When there is no lateral load, the terms Fz and Fy vanish, because these are not the total values, instead they are the contributions due to the load transfer when cornering.

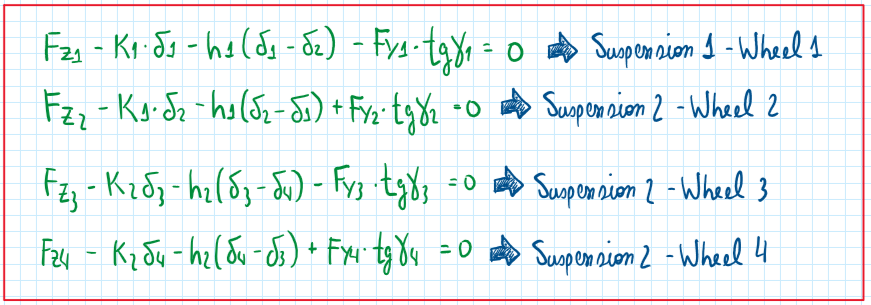
Those four equations are called equilibrium equations. In addition these can also account the five displacements for the lateral dynamics. They are Y, Z, roll (moment around X ), pitch (moment around Y) and yaw (moment around Z).

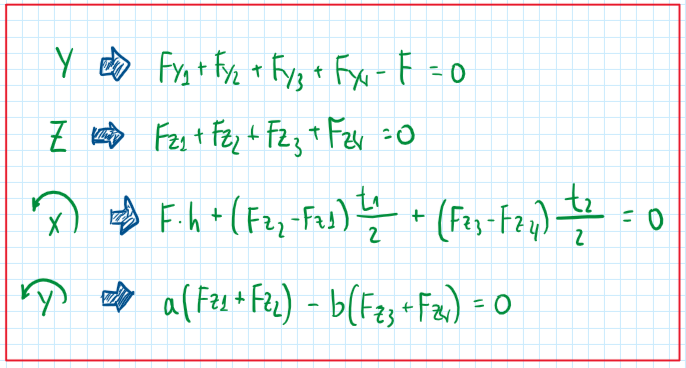
Observing all those equations described before it is possible to account a total of 13 equations with 15 parameters. This enables the solution of the system. Hence some assumptions to simplify this system relative to its equations parameters must be made. The parameters are W, alpha, beta, D1, D2, D3, D4, F_z1, F_z2, F_z3, F_z4, F_y1, F_y2 F_y3, and F_y4, a total of 15 parameters. One option to simplify is to consider the slip angle alpha equal for the wheels of the same axle, thus A₁₂ = A₁₁ = A₁, and this same approach is done from the another axle. An important detail relative to the lateral dynamics is the correlation between Fy and Fz which usually is obtained with tyre data. However these exhibits a nonlinear behavior, for simplification it is usual a linearization of the tire curve.

Considering F_0z2 = mgb/2l, which is the static load from the wheel of the rear axle, the same from the front axle it is given by F_0z1 = mga/2l. This linearization is performed to equalize the number of parameters with the equation ones. Hence these relations can also be written in function of the rear wheels.

Therefore there are two more equations whose completes this system, thus, 15 equations and 15 parameters. As the track and the slip angle are assumed as constant it is possible to write :

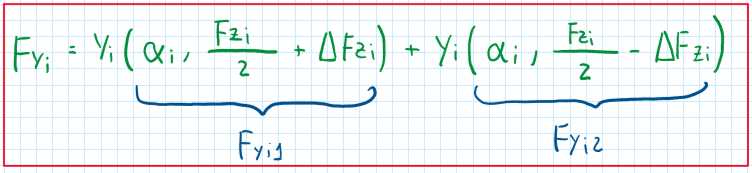
Where F_zi is the total vertical load, delta F_zi is the vertical load transfer and F_yi is lateral force produced by the tires. As can be observed in the equation, the main parameter which F_yi is a function of is delta F_zi, because the others, alpha i and F_zi can be assumed constant, while delta F_zi depends on the maneuver. Therefore it can be written that :

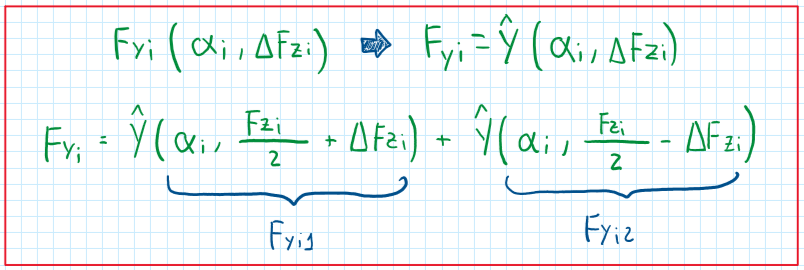
From the F_yi equation above, It is possible to verify a graphical correlation between F_yi, alpha i and F_zi:

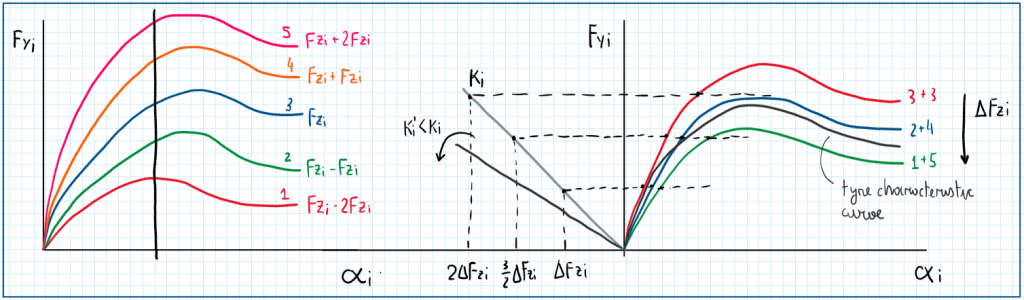
Observing those graphs and with all considerations previously made and the linearization, the behavior of the relation between lateral force and slip angle is not constant. The space between the curves does not increase proportionally to the lateral load transfer. In addition it increases less and less as more lateral load is transferred. If those parameters are all correlated together, it is possible to identify and optimal characteristic curve respective to the tire. Therefore, it can be inferred by those graphics are that the increase of the lateral load transfer decrease the lateral force produced by the tire in a non-linear way. In addition the equation F_yi guarantee that the lateral load transfer and the slip angle are the main parameters which determines the cornering capability. There is no influence of the suspension. However, observing the graph which coordinates F_yi and delta F_zi are correlated, it is possible to affirm that suspension do not interfere on the lateral transfer and the lateral force, but it splits them between the axles and this is the key point in vehicle dynamics. As the roll stiffness is increased, the row load transfer increase, thus the effect is a reduction on the inclination of the line F_yi delta F_zi, thus the lateral force Fyi decreases as the slip angle increases.

References

• Guiggiani, Massimo. The Science of Vehicle Dynamics. Handling, Braking, and Ride of Road and Race Cars. New York, Springer, 2014;
• GILLESPIE, Thomas D, Fundamentals of Vehicle Dynamics, Warrendale, Society of Automotive Engineers, 1992. 470p.