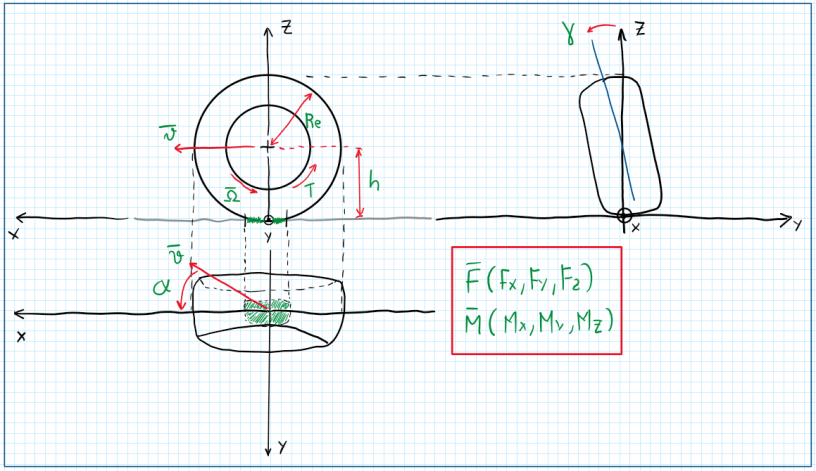
The tires is one of the most important part of the vehicle regarding its movement dynamics. They are also important for comfort aspects. In fact, tires can absorb vibrations and filter deformations due to an important detail, their compliance. Tires can deflect and this changes several characteristics during vehicle operation. For instance, the travel velocity of a tire has no relation with the velocity measured by sensors, because this one account the rim angular velocity. In addition, the tire contact patch is no uniform as it appear, it deforms under every motion of the wheel. This is an important detail, because it affects the point which the forces over the contact patch will result. In general the assumption of displace the forces and account the moments is made without several losses on the quality of the model. Considering the tire model above, it is possible to observe the force and the moment resultant from the contact patch. As these are displaced to the origin O, hence the moments must also be accounted. The main forces are Fx, Fy and Mz. The last one is the self-aligning torque, Mz. The other moments are My, which is the rolling resistance and Mx.

Tire kinematics

The analysis of the tire kinematics is made under some assumptions. Firstly, the camber angle gamma can be considered 0. In fact, it is easy to understood that the tire travel velocity is given by a function of the slip angle alpha. In addition, this is also a source of the tire non-linearities. Hence, it can be written that tire travel velocity:

As the slip angle arises, another component of the velocity V appear, Vy. Hence, with the understanding that the tire is compliant, the angular velocity accounted if from the rim. The angular velocity omega is given by just one component. The main objective of this analysis is to provide a correlation between those velocities, V and omega. In fact, omega is a function of several parameters. Considering the assumption of pure rolling, the results are:

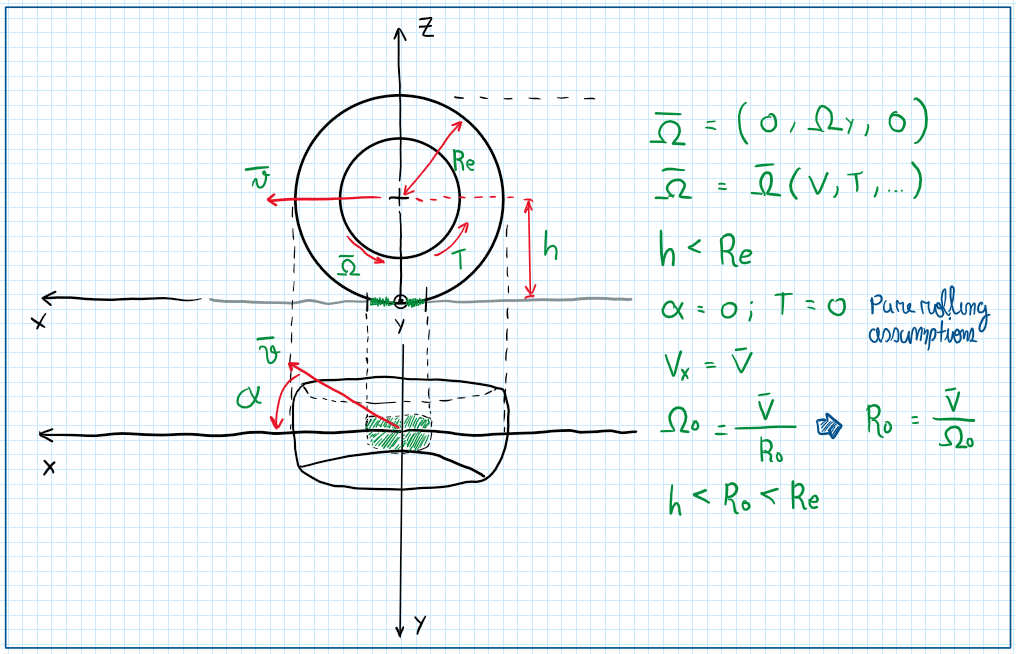
As can be seen, the relation between omega_zero and V results in R_zero which must no be lower than h and higher than Re. This means that the R_zero, which is the distance between the center of the rim until point C, is important for the tire kinematics, because this point is the center of rotation of the wheel. In other words, at point C pass the axis of the instant rotation relative to the ground. However, this point is only valid for solid bodies, thus, the rim.

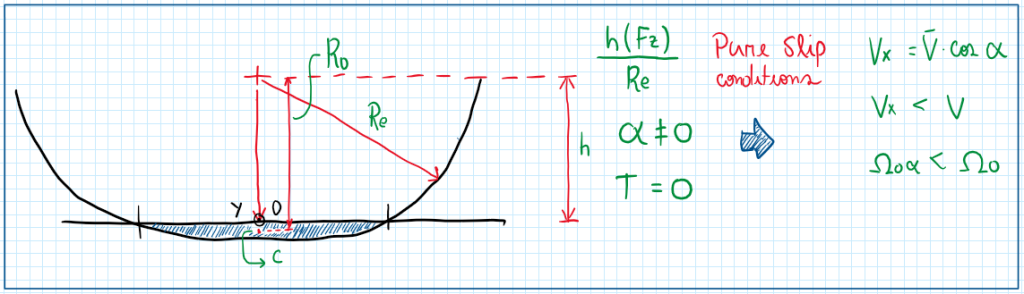
In addition, due to the deformation of the tire contact patch, the compression in this region can be correlated by h/Re. This is a ratio which h is a function of the amount of the vertical load. Hence, adopting the pure slip conditions, the assumptions are that the slip angle (alpha) is different from zero and the torque T is equal to zero. Moreover, the travel velocity is given by Vx which is lower than V. Consequently the angular velocity will also be slower, omega_0_alpha < omega_0. Finally, it can be concluded that:

The term R_0_alpha is a function of the slip angle (alpha), which is not a controlled parameter, because the slip angle depends on several parameters as materials properties and the vertical loads over the tire. As these parameters also change dynamically, it is too time consuming a perfect definition of R_0 during tire operation. Therefore, the point S_alpha is constantly oscillating its position. As the point S_alpha is the axis of instantly rotation of the wheel, the result is helical movement on the Y direction while the vehicle travels on the X direction. Actually, R_0_alpha is almost equal to R_0, but there is a slight difference between them.

Effects of the brake torque

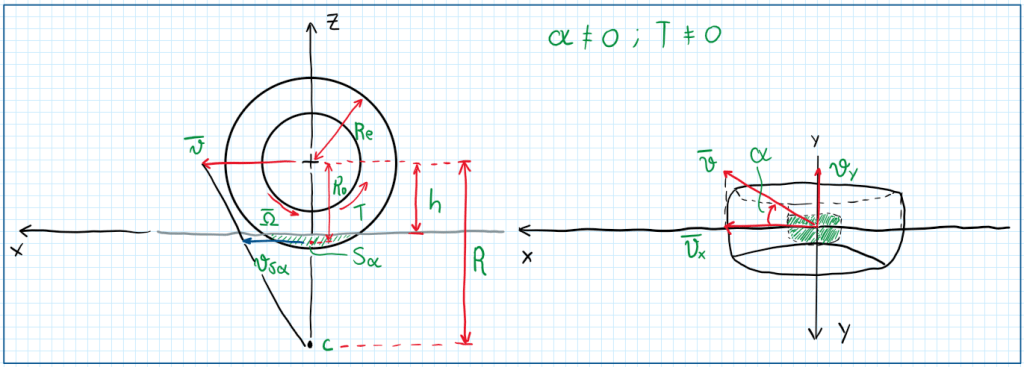
Another situation which must be modelled is the braking movement. In this case, all parameters is accounted, because the slip angle (alpha) and the torque T are different from zero. There are some differences between this case relative to the other, actually the torque T is the most important parameter due to the following relation:

Hence, the axis of instant rotation will be a function of alpha and rotational speed which is decreasing, because of the brake torque T. In addition, omega decreases while R increases. The result is that the point C will be even longer than in the two previous cases. Understanding that these two velocities Vx and Vy exist due to the slip angle (alpha) and a point S_alpha, the ehelical axis of the rotation, a new velocity component arises, Vs_alpha which is the slip velocity. Actually this velocity component arises due to alpha. However, Vsx only appears when a brake torque is applied while the Vsy arises solely due to alpha.

The slip coefficients

A better approach to analyze the wheel slip is the adoption of slip coefficients. These are normalized parameters which characterize the wheel motion. Normalized parameters are used to comparison between different systems, but without the influence of external factors. There are two different slip coefficients, the theoretical and the practical ones. Both quantify the degree of slip and slippage. The practical slip coefficients is a non-dimensional vector:

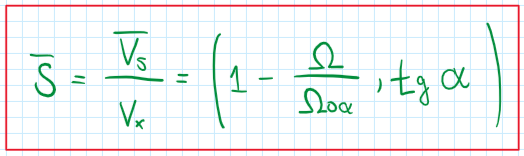
As can be seen, the slip coefficient combines the main parameters which characterize the motion of the wheel, whose are alpha, V and omega. It is possible to identify the results of this coefficient under the situations proposed.

The second kind of non-dimensional parameter is the theoretical slip coefficient:

After the definition of both slip coefficients, it is possible to correlate them:

Therefore, it is possible to define a link between slip (sigma_y) and slippage (sigma_x) coefficients.

Ground forces and moments

As the main parameters are Vs, sigma and S, the moments generated due to the tire contact with the ground are correlated with the slip coefficients, mainly the theoretical slip coefficient. The objective is to find (or define) functions which correlates the slip coefficient with the forces. The problem is that there is no method to define correlations (yet), because these forces and moments are dependent from many variables and environmental conditions. In addition there are the structural tire conditions, which also influence on the variation of the forces. The only approach is the semi-empirical approach to collect big data from the experiment to feed semi-empirical formulas and equations, which the magic formula is one of some examples.

References

• Guiggiani, Massimo. The Science of Vehicle Dynamics. Handling, Braking, and Ride of Road and Race Cars. New York, Springer, 2014;
• GILLESPIE, Thomas D, Fundamentals of Vehicle Dynamics, Warrendale, Society of Automotive Engineers, 1992. 470p.