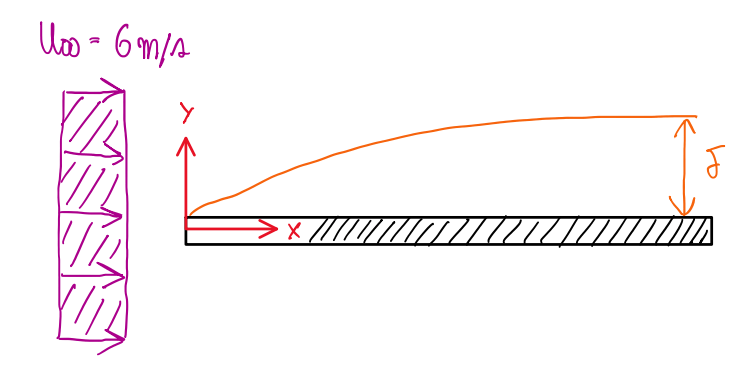
A flat plate is exposed a an air flow with U = 6 m/s, its chord is a = 0.4 m and is displaced parallel to the air flow and at a height y = 0. The Figure that is this the cover of this article illustrates the situation of this exercise.

Part 1 – Skin friction

The first part of this exercise deals with the effects of air viscosity over the flat plate, the vorticity and how the boundary layer thickness and displacements affect the flow.

Question 1 – Calculate the total resistance

q_∞ = ½∙ρ∙U_∞² = ½∙1.2∙6² = 21.6 Pa

Re = U_∞∙x/ν = (6∙0.4)/(15×10^-6) = 160000 = 1.6×10⁵

C_ƒ = 1.328/√Re_L = 1.328/√160000 = 0.00332 = 3.32×10^-3

D_ƒ = C_ƒ ∙ a ∙ q_∞ = 0.00332 ∙ 0.4 ∙ 21.6 = 0.0286848 N/m → Dt = 2 ∙ D_ƒ = 2 ∙ 0.0286848 = 0.0573696 N/m

As can be seen, the drag resistance of a flat plate is very small, even with the contribution of both surfaces of a flat plate, which is the reason why D_ƒ is multiplied by two. Hence, the total drag in a flat plate is the contributions of its both surfaces.

Question 2 – Expresse the vorticity at the upper surface of the flat plate ω(x, y = 0) as a function of x using the following velocity profile

The definition of vorticity is curl of the velocity gradient, that if developed for the flat plate case results in ω_Z ≈ – ∂U/∂y, thus it is possible to write:

U/U_∞ = 2(y/δ(x)) – (y/δ(x))² → U = U_∞[2(y/δ(x)) – (y/δ(x))²]

∂U/∂y = U_∞[2(1/δ(x)) – 2(y/δ(x)²)]

ω_Z ≈ – ∂U/∂y = U_∞[2(1/δ(x)) – 2(y/δ(x)²)] ; y = 0

ω_Z ≈ – 2(U_∞/δ(x))

δ(x) = 4.91∙x/√Re_x = 4.91∙[x/(x∙U_∞/υ)^½] = 4.91 (x^½∙υ^½/U_∞^½)

ω_Z ≈ – 2(U_∞/δ(x)) = – 2{U_∞/[4.91 (x^½∙υ^½/U_∞^½)]} = – (2/4.91)∙(U_∞^3/2/x^½∙υ^½) = – (2/4.91)∙[6^3/2/(0.4∙15∙10^-6)]

ω_Z = – (2/4.91)∙6000 = – 2443.992 m/s

As can be seen, the vorticity exhibited by an airflow when it pass over a flat plate has a very high value. Even though the flow is laminar. This occurs, because the vorticity over a flat plate is very sensible to the velocity and longitudinal length of the flat plate.

Question 3 – Express the volumetric flow rate in an analytic form as a function of x

Through a similar method it is possible to calculate the volumetric flow rate. This parameter is basically an integration of the velocity profile from zero to the boundary layer thickness. However, this method can only be assumed if the flow is uniform and aligned with the longitudinal direction, which is the x coordinate. The flow rate due to the displacement thickness is given by:

q’ = U_∞(δ(x) – δ*(x))

δ^*(x) = ∫₀^{y ≥ δ}(1 – U(y)/U_∞)dy = ∫₀^δ[1 – 2(y/δ(x)) + (y/δ(x))²]dy

δ^*(x) = (δ(x) – 0) – (1/δ(x))(δ(x)² – 0) + (1/3δ(x)²)(δ(x)³ – 0)

δ^*(x) = δ(x) – δ(x) + δ(x)/3

q’ = U_∞(δ(x) – δ(x)/3) = 2(U_∞∙δ(x))/3

δ(x) = 4.91∙x/√Re_x = 4.91 x/(U_∞∙x/ν)^½

q’ = 3.273√(U_∞∙x∙ν) = 0.01964 m²/s

As can be seen, the mass flow rate depends on x, U_∞ and the fluid properties.

Part 2 – Angle variation

The next section of this exercise proposes an inclination of the flat plat, more precisely α = 0.1 rad relative to the horizontal plane. The lift exhibited is L’ = 5.0 N/m and the absolute viscous force τ at the flat plate is 0.1 N/m.

Question 4 – Calculate the lift contribution due to the viscous forces

L_ƒ = τ∙sin(α) = 0.1∙sin(0.1) = 0.0099 ≃ 0.01 N/m → L_ƒ = – 0.01 N/m

L’ = L_P + L_ƒ → L_P = L’ – L_ƒ = 5.0 – (-0.01) = 5.01 N/m

The effect due to the air friction are negligible if compared with the effects due to the form lift, also called lift due to pressure.

Question 5 – Calculate the drag contribution due to viscous effects and form

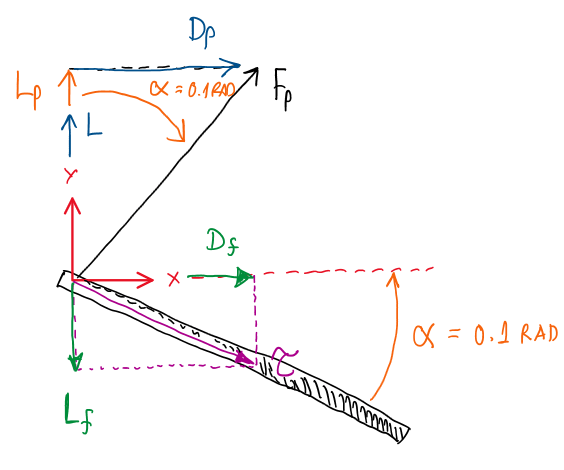
sin(α) = D_P/F_P ; cos(α) = L_P/F_P ; FP = (D_P/sin(α)) = (F_P/cos(α))

D_P = L_P∙tg(α) = 5.01∙Tg(0.1) = 0.503 N/m

D_ƒ = τ∙cos(α) = 0.1∙cos(0.1) = 0.0995 ≃ 0.1 N/m

D = D_ƒ + D_P = 0.1 + 0.503 = 0.603 N/m

This calculation is important to understand the components produced by a wing or a flat plate. These are described below:

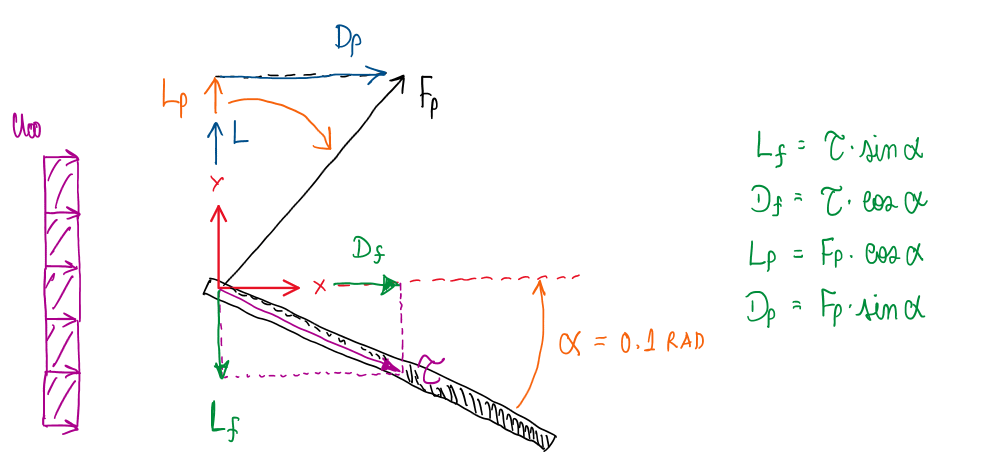
Hence, it is possible to notice that the forces acting on a wing is all a matter of geometry and trigonometry (Figure 3).

Part 3 – The effects of the form

The final section of the exercise proposes a massive slope for the flat plate α = π/2 rad. The objective is to calculate the pressure coefficient and understand the impact of the shape on the aerodynamics.

Question 6 – Calculate the average C_P at the front of the flat plate

The pressure coefficient at the base C_P,b = – 7/4 and the drag coefficient C_D = 2.0. In this case, a plate at 90°, it is possible to assume that CD is the resultant between pressure coefficient at the front and at the base, thus:

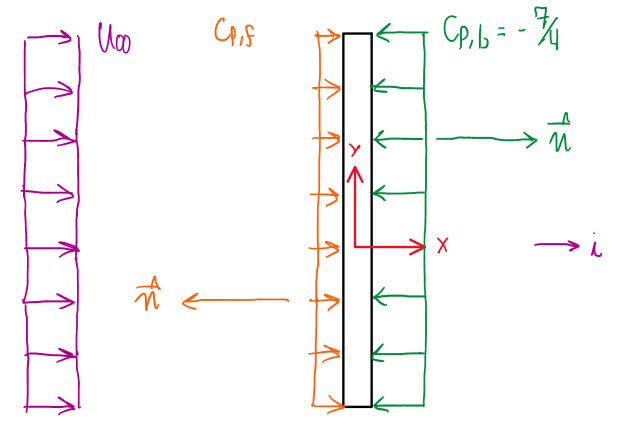
-q_∞∙∫C_P∙n∙i∙ds → Equation for the pressure force

D_b = -q_∞∙∫C_P,b∙n∙i∙ds = -q_∞∙∫C_P,b∙(1)∙a∙dL_Z = -q_∞∙C_P,b∙a

D_f = -q_∞∙∫C_P,f∙n∙i∙ds = -q_∞∙∫C_P,f∙(-1)∙a∙dL_Z = q_∞∙C_P,f∙a

D = q_∞∙C_D∙a = D_b + D_f = -q_∞∙C_P,b∙a + q_∞∙C_P,f∙a

q_∞∙C_D∙a = -q_∞∙C_P,b∙a + q_∞∙C_P,f∙a

C_D = – C_P,b + C_P,f → C_P,f = C_D + C_P,b = 2.0 – 7/4 = ¼ = 0.25

Question 7 – Calculate the torque about the z axis in (x = 0 , y = 0)

Considering the frontal CP is asymmetrically distributed and this is described by the following equation:

C_P = 1 – 9(y²/a²) – (y/a)

The procedure to calculate the torque begins with the calculation of the maximum and minimum torque at the front of the plate according to Figure 4.

C_P,f(a/2) = 1 – 9(a/2)²/a² – (a/2)/a = 1 – 9/4 – 1/2 = 1/2 – 9/4 = – 7/4

C_P,f(-a/2) = 1 – 9(-a/2)²/a² – (-a/2)/a = 1 – 9/4 + 1/2 = 3/2 – 9/4 = – 3/4

M_Z = ∫q_∞∙C_P∙y∙dy = ∫_-a/2^a/2q_∞∙C_P,f∙y∙dy = q_∞∫_-a/2^a/2(1 – 9y²/a² – y/a)∙y∙dy

MZ = q_∞[½(a²/4 – a²/4) – (9/4a²)∙(a⁴/16 – a⁴/16) – (1/3a)∙(a³/8 + a³/8)] = – (q_∞∙a²)/12

M_Z = -(21.6∙0.4²)/12 = 0.288 (Nm)/m

Conclusion

Probably the most important conclusion of this exercise is about the effects of plate slope. In the beginning of the exercise the plat is at α = 0 and the only aerodynamic forces are due to the friction between the air and the plate surfaces. As soon the plate exhibit some slope, other aerodynamic force components arise, these are respective to the shape of the plate. It could be a wing, so the shape of it accounting the area along the wing span. In addition, this kind of aerodynamic forces are higher in magnitude when compared with the components due to friction, because the are related to pressure, more precisely, the dynamic pressure and the pressure coefficient. In other words, velocity and atmospheric pressure. It could be possible to clay that aerodynamics forces are all about velocity, despite other parameters as wing span, wing angle, chord and fluid properties, but velocity has huge importance in those calculations.

Download

• Click here to download the hand notes of this exercise.